все сигналы обладают одинаковой энергией (длины всех векторов одинаковы);
между всеми сигналами одинаковы и максимальны. Сигналы, удовлетворяющие этим условиям, называются . Для такой системы сигналов после ее нормировки все элементы на
главной диагонали матрицы Грама (1.47) равны единице, а все остальные элементы также принимают одно и то же значение . Найдем это значение.
Очевидно, что справедливо неравенство
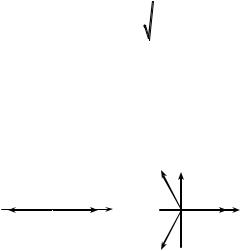
На рис. 2.22 изображены симплексные системы векторов для = 2 и = 3. При М = 2 векторы соответствуют двум противоположным сигналам. Именно такие сигналы формируются при ФМ (рис. 2.18а). Таким образом, метод ФМ занимает особое место среди других методов модуляции в двоичных системах.
Рис. 2.22. Симплексные системы векторов для =2 и =3
Во-первых, если реализованы оговоренные выше условия, он должен обеспечить минимально-возможную вероятность ошибки при приеме двоичного сигнала.
Во-вторых, он широко используется при генерировании различных си-
Итак, для одного частного идеализированного случая мы решили задачу статистического синтеза всей системы передачи информации, и уже на этом примере увидели те трудности, которые придется преодолеть при практической реализации оптимальной СПИ.
Во-первых, это трудности при генерировании самих сигналов, но, как уже отмечалось, они частично преодолеваются путем использования сиг- нально-кодовых конструкций.
Во-вторых, каждый сигнал из системы, содержащей = 2таких сигналов, занимает довольно широкую полосу частот. Необходимая полоса была бы намного меньше, если бы то же сообщение передавалось обычным способом при помощи комбинации, состоящей из двоичных символов.
В-третьих, провести обработку принимаемого сигнала в соответствии с выражением (2.44) можно при помощи корреляционного приемника. В итоге в пункте приема нужно иметь параллельно работающих корреляционных приемников, каждый из которых настроен на прием своего сигнала. Эта процедура называется “прием сигнала в целом”.
В-четвертых, если условия работы СПИ начать приближать к реальным (неравновероятность сигналов на выходе источника информации; нестабильность параметров устройств, генерирующих и обрабатывающих сигналы; наличие мультипликативной помехи и т.п.), задача статистического синтеза всей СПИ становится неразрешимой.
Это еще раз подтверждает мысль, высказанную в разд. 2.1: сложную задачу по необходимости приходится разбивать на ряд более простых задач, то есть обработку сигналов и в процессе передачи, и в процессе приема проводить поэтапно, при этом нет полной уверенности в том, что на каждом этапе мы идем к конечной цели кратчайшим путем.
аналого-цифрового преобразования непрерывного сигнала.
Изобразите обобщенную модель системы передачи информации. Опишите функции кодера и декодера.
Приведите несколько примеров преобразователей сообщения в первичный сигнал.
Зачем нужна модуляция? Назовите виды аналоговой модуляции гармонической несущей.
Назовите способы манипуляции гармонической несущей. Чем обусловлен выбор того или иного способа?
Каковы недостатки многопозиционных методов манипуляции гармонической несущей?
Из каких соображений выбирается шаг квантования непрерывного сигнала: по напряжению?
Из каких соображений выбирается шаг квантования непрерывного сигнала:по времени?
10.Дайте определения терминов: сообщение, сигнал, помеха, канал связи, линия связи, многоканальная связь, многостанционный доступ, техническая скорость передачи.
11.Почему шаг квантования непрерывного сигнала по времени выбирается меньше того значения, которое следует из теоремы отсчетов?
12.Укажите стандартную частоту квантования во времени (отсчетов/с) телефонного сигнала.
13.Укажите количество разрядов в стандартном АЦП, применяемом при преобразовании телефонного сигнала.
14. Что удобнее применять на практике –коррелятор или согласованный фильтр?
3 КОДИРОВАНИЕ КАНАЛА.
3.1 Корректирующие коды
случае говорят, что в данном символе произошла ошибка. Ошибки возникают случайным образом, поэтому нет гарантии того, что в принятом сигнале они отсутствуют.
В таких условиях дальнейшая обработка (декодирование) цифрового сигнала с выхода демодулятора основана на анализе взаимосвязи между символами в последовательности. Если декодер приходит к выводу, что такая последовательность символов в принципе не могла быть передана, то такое решение называется . На данном этапе декодер не пытается выяснить, какие именно символы приняты ошибочно и каковы их истинные значения, важно лишь установить факт, что в принятой последовательности хотя бы один символ содержит ошибку. Таким образом, этап обнаружения ошибок завершается выдачей решения в двоичной форме: “нет ошибок”, “есть хотя бы одна ошибка”. Если принято первое решение, декодирование очередной принятой последовательности на этом фактически завершается.
Если в системе передачи информации отсутствует обратный канал, то есть, нет возможности сообщить в пункт передачи о принятом решении, декодер после обнаружения ошибок предпринимает попытку восстановить переданное сообщение. Если ему удалось угадать положение ошибочных символов и их истинные значения, считают, что произошло .
Очевидно, что угадывание далеко не всегда завершается успехом, поэтому не все возможные сочетания ошибок могут быть исправлены и даже обнаружены. В итоге иногда на выходе декодера всё-таки будут появляться последовательности символов, содержащие ошибки. Поэтому основной задачей теории помехоустойчивого кодирования является поиск таких последовательностей символов, при использовании которых процент ошибочных комбинаций на выходе декодера был бы как можно ниже.
корректирующим называется такой код, использование которого даёт возможность в процессе приёма цифрового сигнала обнаруживать в нём наличие ошибок и, возможно, даже исправлять некоторые из ошибочных символов.
Среди корректирующих кодов наибольшее распространение получили блочные двоичные коды, то есть передача двоичного сообщения производится блоками, причём каждый блок содержит двоичных символов. Кодирова-
ние и декодирование каждого блока производится независимо от других блоков.
Напомним, что (1.43) между двумя кодовыми
комбинациями и численно равно количеству символов, в которых эти комбинации отличаются одна от другой. Например, пусть =5, =01101, =00001, тогда .
равен количеству единиц, содержащихся в ней. Например, W()=3, W()=1. Очевидно, что 0≤W≤.
Расстояние Хэмминга удобно вычислять, пользуясь операцией сумми-
В дальнейшем суммирование двоичных кодовых комбинаций или их элементов предполагается проводить лишь по mod 2, даже если используется обычный знак суммирования.
– это -разрядная двоичная комбинация, в которой положение единиц указывает на положение ошибочных символов в принятой
Например, если =6, =011010, =010100, то =001110.
Кратность ошибки q – это количество ошибочных символов в принятой комбинации
Величина случайна, в каналах с независимыми ошибками её математическое ожидание =, где – вероятность появления ошибки в одном символе на выходе демодулятора (битовая вероятность ошибки). В реальных каналах связи отношение сигнал/помеха обычно настолько велико, что <<1. Это значит, что большинство комбинаций будут приняты без ошибок (=0), изредка будут встречаться комбинации, содержащие где-то один ошибочный символ (=1), ещё реже – комбинации с двукратными ошибками и т.д. То есть, принятая комбинация лежит недалеко от переданной.
Очевидно, что никакой код не способен обнаружить и исправить все возможные ошибки вплоть до =. Возможности любого кода ограничены, поэтому в первую очередь нужно направить усилия на борьбу с теми видами ошибок, которые встречаются наиболее часто, то есть с ошибками малых кратностей.
Способ кодирования полностью определён, если задана
Таблица 3.1 – Пример кодовой таблицы (=6)
, в которой перечислены все возможные сообщения и соответствующие им -разрядные кодовые комбинации. Например, если каждая комбинация соответствует одной букве алфавита, а в используемом алфавите всего 4 буквы, кодовая таблица может иметь следующий вид (табл.3.1).
Можно вычислить расстояние между двумя любыми комбинациями в кодовой таблице. Минимальное его значение называется кодовым расстоянием и служит одной из важнейших характери-
стик выбранного способа кодирования. Это показатель отличия двух наиболее близких комбинаций в таблице. В приведённом примере
Довольно трудоёмкий, зато универсальный способ декодирования – это
декодирование по минимуму расстояния. Принятая комбинация сравнивается поочерёдно со всеми комбинациями в таблице. Если такая комбинация есть в таблице, то декодирование заканчивается. Конечно, при этом нет полной уверенности в том, что в принятой комбинации отсутствуют ошибки, хотя это весьма вероятно. Просто здесь нет лучшего варианта, поскольку обычно равновозможна передача любой из комбинаций, входящих в таблицу.
В противном случае (принятая комбинация не совпадает ни с одной комбинацией в кодовой таблице) следует несомненный вывод: в принятой комбинации есть ошибка и, может быть, не одна (произошло обнаружение ошибок).
Логически рассуждая и рассматривая примеры, легко убедиться в том,
можно гарантированно обнаруживать любые ошибки кратности
приведённом примере (табл. 3.1) код обнаруживает все однократные
двукратные ошибки. Этот же код способен обнаруживать также некоторые ошибки более высоких кратностей, но не все. В частности, ошибки в первых трёх символах кодовой комбинации не будут замечены.
После обнаружения ошибок в СПИ с обратным каналом посылают запрос на повторную передачу данной комбинации. При отсутствии канала переспроса следует попытаться исправить ошибки, то есть найти в кодовой
таблице комбинацию, наиболее близкую к той, которая была принята (наиболее правдоподобную). Даже если в таблице нашлась лишь одна такая комбинация, это ещё не служит гарантией того, что ошибки исправлены верно.
Можно гарантированно исправить любые ошибки кратности
Например, код (табл. 3.1) способен исправить любую однократную ошибку. Убедитесь на примерах в том, что ресурсы кода используются полнее, если является нечётным числом. Кроме того, видно, что исправлять
ошибки труднее, нежели их обнаруживать. Разумеется, возможны случаи, когда исправляются некоторые ошибки более высоких кратностей, чем следует из (3.6), но не все.
3.2 Линейные блочные коды
Когда количество символов в кодовой комбинации велико (на практике оно может составлять несколько тысяч), кодовая таблица блочного кода может содержать огромное количество комбинаций. Кодирование и декодирование оказываются слишком трудоёмкими. Поэтому вполне естественно желание разработать такие коды, которые позволяют проводить эти операции, не обращаясь к кодовой таблице, а используя лишь некий набор свойств, присущий всем комбинациям в кодовой таблице. Именно такую возможность предоставляет применение линейного блочного кода.
Любой линейный блочный код обозначается как ()-код, где: — количество информационных символов, то есть длина двоичной комбинации, поступающей на вход кодера; — количество символов в комбинации на его выходе. На вход кодера может поступать любая –разрядная комбинация. Число таких комбинаций равно
Если бы кодирование не проводилось (=, то есть входная комбинация сразу поступает на выход кодера), такой код не обладал бы никакими корректирующими свойствами, поскольку для него , и любые ошибки в при-
нятой комбинации оказались бы незамеченными.
бавляет к ним ещё один, проверочный символ (напоминаем об операции mod2)
статочно провести общую проверку на чётность
Если проверка прошла ( 0), то это лишь означает, что такая комбинация могла быть передана. Если же проверка не прошла ( 1), то в принятой комбинации, несомненно, есть ошибки.
Кодовое расстояние для кода с проверкой на чётность равно двум, поэтому в соответствии с (3.5) он обнаруживает любую однократную ошибку. Более того, он способен обнаружить любую ошибку нечётной кратности, но исправлять ошибки он не может.
Операции (3.8) и (3.9) – чрезвычайно простые. Для реализации каждой из них достаточно иметь один счётный триггер. Тогда сразу возникает идея для повышения корректирующей способности кода использовать не одну, а несколько проверок на чётность. При этом очевидно, что в каждой проверке участвуют не все символов, а лишь их часть. А в разных проверках должны участвовать разные группы символов.
В качестве примера рассмотрим код (5,2). Зададим его в , то есть первые символов выходной комбинации должны повторять входные информационные символы, а на оставшихся =-=3 позициях размещаются проверочные символы, которые предстоит вычислить при
где – вектор-строка информационных символов, – вектор-строка проверочных символов. В частности, рассмотренный выше простой код с проверкой на чётность тоже является систематическим.
Итак, для кода (5,2) из всевозможных пятиразрядных комбинаций в кодовую таблицу включим лишь такие комбинации, которые удовлетворяют всем трём заданным проверкам на чётность (количество проверок на чётность всегда равно ). Результаты проведения этих проверок для конкретной комбинации представим в виде вектора-строки ко-
торый имеет медицинское название “синдром”, то есть, сочетание признаков, характеризующих определённое состояние. Допустим, для нашего кода мы выбрали следующую систему проверок
1 1 32 1 2 4 3 2 5
то есть, в первой проверке участвуют символы, стоящие на первой и третьей позициях, и т.д. В кодовую таблицу (типа табл. 3.1) включим лишь те комбинации, для которых вектор =. Оказывается, что их всего 4, как и следовало

Таблица 3.2. Кодовая таблица кода (5,2)
По приведённой таблице (табл. 3.2) легко найти, что , то есть за-
данная нами система проверок на чётность (3.11) действительно однозначно определяет систематический корректирующий код, способный не только обнаружить любые однократные и двукратные ошибки, но даже исправлять все однократные ошибки.
1 2 3 4 5
Первая Вторая Третья
Рис. 3.1. Схема проверок на чётность для кода (5,2)
Первый этап декодирования – обнаружение ошибок – фактически сводится к проведению проверок на чётность (3.11) в принятой кодовой комбинации. Считается, что ошибок нет, если =.
Если ≠, второй этап – исправление ошибок – также можно провести, пользуясь схемой рис.3.1 и рассматривая различные варианты. Например, если принята комбинация =11110, то находим =011 и делаем вывод о наличии ошибок в принятой комбинации. Исходя из возможностей данного кода ( ), делаем предположение, что произошла однократная ошибка (гаран-
тированно исправлять ошибки более высоких кратностей этот код все равно не может (3.6)). Рассматривая разные варианты расположения этой одиночной ошибки, видим, что наблюдаемый результат =011 мог быть получен лишь в случае, когда эта ошибка расположена во втором символе, следовательно, =10110 и =10.
Чтобы не перебирать различные варианты каждый раз при декодировании очередной кодовой комбинации, полезно заранее заготовить таблицу, в которой перечислить все возможные векторы исправляемых ошибок (однократных в нашем примере) и соответствующие им значения вектора-
синдрома (табл. 3.3). Если бы код был способен исправлять ещё и все двукратные ошибки, в эту таблицу следовало бы включить дополнительно векторов таких ошибок, в частности 11000, 10100 и т.д.
Таблица 3.3. Таблица соответствия вектора ошибки и синдрома для (5,2)-кода
Из табл. 3.3 видно, что анализируемый код (5,2) действительно способен исправить любую однократную ошибку, поскольку все значения различны, а каждому соответствует единственный вектор ошибки . Легко убедиться, что для двукратных ошибок такого однозначного соответствия уже не будет.
Чтобы завершить обсуждение тех вычислений, которые нужно проводить при кодировании и декодировании линейных блочных кодов, полезно продолжить их формализацию, в частности, ввести для них более компактную форму записи.
Вместо схемы рис. 3.1 удобно использовать , содержащую строк и столбцов и состоящую из 0 и 1. Каждая строка соответствует одной проверке на четность, причем положение единиц в этой строке указывает на позиции символов кодовой комбинации, участвующих в данной проверке. Для рассмотренного кода (5,2) такая матрица имеет вид
Если линейный блочный код к тому же является систематическим, матрицу можно условно разделить на два блока =(), причем левый блок имеет размеры (), а правый блок — это единичная матрица (). Для нашего примера
где — транспонированная матрица .

Мы обязательно должны вызвать конструктор базового класса , в противном случае фигура не будет проинициализирована! Это делается явным образом: . Если вы помните, в классе конструктор занимается отображением фигуры на экране.
Наконец, мы дошли до реализации (переопределения) абстрактных функций и . Они-то и должны брать на себя основную работу по отображению круга на экране. Если в классе мы еще не имели информацию о том, как именно следует прорисовывать фигуру, то в классе это должно быть абсолютно ясно.
В этом и заключается суть полиморфизма и абстрагирования: метод определяется в месте, где программист имеет наиболее полную информацию, как именно он должен работать.
В реализации класса из листинга 33.8 мы не приводим реальный код рисования круга; все-таки для Web-программирования и PHP традиционный пример с геометрическими фигурами не совсем типичен (зато он прост). Для того чтобы все же иметь возможность отладить код, мы выводим в браузер все действия, которые должна совершить программа («рисуем круг»/»стираем круг» с указанием координат и реального радиуса отображения).
Виртуальный метод не обязательно должен быть абстрактным. Довольно распространена ситуация, когда он сам выполняет некоторые действия и даже вызывается из переопределенного метода по той самой схеме, которую мы рассматривали при обсуждении метода переопределения функций.
Давайте рассмотрим, как использовать наш новый класс (листинг 33.9).
Листинг 33.9. Файл shapes/test.php
<?php ## Проверка виртуальных методов.
Вначале создаем круг. $shape = new Circle();
Далее мы можем «забыть», что $shape — это в действительности
Результатом работы этого скрипта будут строки:
Рисуем круг: (0, 0, 100)

Стираем круг: (101, 6, 200)
Если мысленно представить, как эти операции будут выглядеть на экране, то нетрудно увидеть общую картину: вначале на координатах (0, 0) появился круг радиусом 100 пикселов, затем он передвинулся на координаты (101, 6) и, наконец, увеличился в 2 раза. По окончании работы программы круг с экрана пропал, будто бы его и не было («аннигилировал»).
Для закрепления материала снова взгляните на определение класса из листинга 33.7. Итак, хотя метод запускает , вызывается не
Shape::show(), а функция show() CircleCircle::show()
просто переопределил функцию .
Напоминаем еще раз, что функция, переопределяемая в производном классе, называется виртуальной.
Главное преимущество, которое дает наследование и полиморфизм, — это беспрецедентная легкость создания новых классов, ведущих себя сходным образом с уже существующими. Обратите внимание на то, что добавить в программу новую геометрическую фигуру (например, квадрат) крайне просто: достаточно лишь написать ее класс, сделав его производным от . После этого любая программа, которая могла работать с кругами, начнет работать и с квадратами, «ничего не заметив». Единственное изменение, которое придется внести в код, — это создание объектаквадрата (вместо круга), но тут уж ничего не поделать: если вы хотите что-то создать, вы должны четко знать, что именно это будет.
Абстрактные классы и методы
До сих пор мы употребляли термины «абстрактный класс» и «абстрактный метод», не вдаваясь особенно в детали. Давайте посмотрим, какими основными свойствами обладают эти «абстракции».
Абстрактный метод нельзя вызвать, если он не был переопределен в производном классе. Собственно, написав функцию и поместив в нее вызов , мы как раз и гарантируем, что она обязательно будет переопределена в производном классе (иначе получим ошибку во время выполнения программы).
Объект абстрактного класса, очевидно, невозможно создать. Действительно, представьте, что мы записали оператор: $obj = new Shape(). Что при этом должно произойти? Ведь фигура не знает, как себя рисовать — об этом заботятся производные классы.

Любой класс, содержащий хотя бы один абстрактный метод, сам является абстрактным. Действительно, если предположить, что кто-нибудь создаст объект этого класса и случайно вызовет абстрактный метод, получим ошибку.
Специально для того, чтобы автоматически учесть эти особенности, в объектноориентированных языках программирования Java и PHP 5 введено ключевое слово — модификатор . Вы можете объявить класс или метод как , и тогда контроль за их некорректным использованием возьмет на себя сам PHP.
Абстрактные классы можно использовать только для одной цели: создавать от них производные. В листинге 33.10 приведен все тот же самый класс , но только теперь мы используем ключевое слово там, где это необходимо по логике.
Листинг 33.10. Файл shapes/ShapeA.php
// Абстрактные методы.
abstract protected function hide(); abstract protected function show();
Как видите, при объявлении абстрактного метода (например, ) вы уже не должны определять его тело — просто поставьте точку с запятой после его прототипа.
Если вы случайно пропустите ключевое слово в заголовке класса , PHP напомнит вам об этом сообщением о фатальной ошибке:
: Class Shape contains 2 abstract methods and must therefore be declared abstract (Shape::hide, Shape::show)

Совместимость родственных типов
Пусть у нас есть базовый класс и производный от него — . В соответствии с идеологией наследования, везде, где может быть использован объект типа , возможно и применение -объекта, но не наоборот! В самом деле, если мы неявно «преобразуем» в , то сможем работать с его — частью (свойствами и методами): ведь любой круг является также и фигурой. В то же время, преобразовать в нельзя: ведь имея объект типа , мы не знаем, круг ли это, квадрат или треугольник (при условии, что эти классы объявляются в программе).
Мы приходим к правилу совместимости типов, существующему в любом объектном языке программирования: объекты производных классов допустимо использовать в том же контексте, что и объекты базовых.
Уточнение типа в функциях
В предыдущей главе мы уже говорили о том, что при определении функций и методов допустимо указывать типы аргументов-объектов. В роли таких типов всегда выступают имена классов. Данный механизм называется уточнением типа. Рассмотрим пример:
$shape = new Circle(); moveSize($shape);
Данный код корректен: мы передаем функции moveSize() Circle, что совпадает с именем класса в прототипе процедуры. Но задумаемся на мгновение: ведь функции moveSize(), по сути, совершенно все равно, с фигурой какого типа она работает. Действительно, методы moveBy() resizeBy() существуют у любой фигуры, и их допустимо применять к произвольным объектам, базовый класс которых — Shape
Руководствуясь данными рассуждениями, модифицируем код (листинг 33.11).
Листинг 33.11. Файл shapes/cast.php
<?php ## Уточнение и совместимость типов. require_once «Circle.php»;
Мы увидим, что он прекрасно работает: вместо аргумента типа можно подставлять объект класса .

Проверка совместимости типов производится во время выполнения программы, а не во время ее трансляции. Если мы попробуем вызвать , то получим такое сообщение:
: Argument 1 must be an object of class Shape
Листинг 33.12. Файл shapes/instanceof.php
$class = «Shape»;
if (!($obj instanceof $class))
Вместо , конечно, можно и явно написать . Мы просто хотели продемонстрировать, что с помощью допустимо использовать имя класса, заданное неявно (в переменной).
Обратное преобразование типа
При помощи оператора можно определять, каким набором свойств и методов обладает тот или иной объект, и выполнять в зависимости от этого различные действия. Например:
Здесь можно вызвать специфичные для Circle методы,
отсутствующие в базовом классе Shape.
Данный код, конечно, не является лучшим примером, потому что он не позволяет в будущем легко добавлять новые фигуры в программу. Собственно, полиморфизм как раз и был изобретен для того, чтобы избежать подобных -конструкций в программе, заменив их вызовами виртуальных методов. Тем не менее в некоторых ситуациях подобный подход все же находит применение.

Множественное наследование и интерфейсы
До сих пор мы подразумевали, что у каждого производного класса может быть только единственный базовый. Наследовать свойства и методы сразу нескольких классов (например, писать class A extends B, C, D) в PHP нельзя.
Тем не менее в Zend Engine 2 заложена возможность реализации множественного наследования. Она просто не задействуется в PHP.
Большинство современных языков программирования (Java, C# и т. д.) отказались от реализации множественного наследования, потому что она очень сильно усложняет логику программы и добавляет много неоднозначностей в код. Например, что делать, если класс наследуется от двух других, имеющих методы с одинаковыми именами? Который из них будет использоваться по умолчанию? Существуют и другие неоднозначности, гораздо более серьезные.
Необходимо заметить, что некоторые языки программирования со значительной историей (C++, Perl) все же поддерживают множественное наследование.
В последнее время на смену идеологии множественного наследования пришел другой, упрощенный метод: использование интерфейсов. Интерфейс () представляет собой обычный абстрактный класс, но только в нем не может быть свойств, и, конечно, не определены тела у методов. Фактически некоторый интерфейс указывает лишь список методов, их аргументы и модификаторы доступа (обычно только и ). Допускается также описание констант внутри интерфейса (ключевое слово ).
Класс, наследующий некоторый интерфейс (или, как говорят, реализующий его), обязан содержать в себе определения всех методов, заявленных в интерфейсе. Это объясняет, почему в мире ООП интерфейс часто называют контрактом: любой класс, «подписавшись в контракте», обязуется «выполнять» его «условия». Если хотя бы один из методов не будет реализован, вы не сможете создать объект класса: возникнет ошибка.
Главное достоинство заключается в том, что класс может реализовывать (наследовать) сразу несколько интерфейсов. Для «привязки» интерфейсов к классу используется ключевое слово :
public function getCoord(); // тело не указывается!
public function getNumWheels(); // возвращает число колес

Некоторые программисты предпочитают начинать имена интерфейсов с заглавной буквы I, чтобы отличить их от классов. Это, конечно, не обязательно.
Множественная реализация интерфейсов
Интерфейсы могут также наследовать (расширять) друг друга. Взгляните на листинг 33.13.
Листинг 33.13. Файл ifacemulti.php
<?php ## Множественное наследование интерфейсов. // Сущность: «материальный объект».
public function getCoord(); // возвращает координаты объекта // Обратите внимание, тело метода не указывается!
Сущность: «транспортное средство». ВНИМАНИЕ: при расширении
интерфейсов нужно использовать ключевое слово extends, а не
public function getNumPassengers(); // максимальное число пассажиров
«Запорожец» — это: транспортное средство с колесами, существующее
в материальном мире.
// Также нужно определить конструктор, деструктор и другие методы.
Из этого кода явно напрашивается вывод: интерфейсы часто используются как средство классификации объектов в программе. Для каждого абстрактного типа объекта из предметной области создается собственный интерфейс, а затем, при описании новых классов, указывается, какие интерфейсы они реализуют — иными словами, как их можно классифицировать. На примере класса хорошо видно: при

помощи интерфейсов мы даем «толкование» классу-термину, как будто бы описываем его в толковом словаре. Это толкование — поведенческое: мы описываем, что «Запорожец» должен «уметь делать».
Обратите внимание на одну деталь. Интерфейс расширяется интерфейсом , который, в свою очередь, реализуется классом . В то же время, реализует и напрямую. Получается, что у «Запорожца» имеются две реализации интерфейса «материальный объект»: непосредственный и через «транспортное средство». Такая ситуация довольно типична и является совершенно корректной: если некоторый интерфейс реализуется дважды, то в действительности в классе имеется лишь одна «ссылка» на него. Таким образом, никакого конфликта нет.
Кстати, если бы вместо интерфейсов использовалось множественное наследование, как в C++, то мы получили бы большую проблему: двойное включение класса. За счет крайней «легковесности» интерфейсов в языках PHP, Java и C# этого неприятного вопроса просто не возникает.
Интерфейсы и абстрактные классы
В случае если класс подключает к себе интерфейсы, но реализует не все методы в них, он автоматически становится абстрактным. Взгляните на листинг 33.14.
Листинг 33.14. Файл abstract.php
public function F();
Если мы пропустим ключевое слово в описании класса, то получим уже знакомое нам сообщение:
: Class C contains 1 abstract methods and must therefore be declared abstract (I::F)
Это и не удивительно: ведь мы не можем создать в программе объект класса, в котором отсутствует один из методов, а такой класс как раз и называется абстрактным.
В этой главе мы продолжили знакомство с миром объектно-ориентированного программирования и узнали о двух взаимосвязанных концепциях — наследовании и полиморфизме, без которых ООП немыслимо так же, как оно немыслимо без ин-
капсуляции. Мы научились обращаться из производных классов к членам базовым, и, что гораздо более важно, из базовых — к производным, что позволило использовать механизм абстракции и полиморфизма. Мы познакомились с понятием совместимости типов и оператором , а также идеологией интерфейсов.
Для детального ознакомления с идеями объектно-ориентированного программирования мы настоятельно рекомендуем вам почитать специализированную литературу, например любую книгу по Java или труды Бьерна Страуструпа, автора языка C++.

Обработка ошибок и исключения
Листинги данной главы можно найти в подкаталоге except.
В программистском мире идеология исключений известна довольно давно, и в PHP версии 5 наконец-то появилась ее полноценная поддержка. В этой главе мы кратко рассмотрим основы технологии, а также приведем примеры использования исключений.
Что такое ошибка?
В программистском фольклоре имеется одна шутка, принадлежащая кому-то из ве-
ликих. Она звучит так: «В любой программе есть хотя бы одна ошибка». Если гово-
рить серьезно, то на практике «хотя бы одна» обычно означает «много» или даже «очень много».
При программировании на любом языке фаза «избавления» программы от разного рода ошибок (иными словами, фаза отладки) является наиболее длительной и трудоемкой. Так что, если вы раньше не программировали много, приготовьтесь к тому, что основное времяпровождение программиста — это борьба с ошибками.
Термин «ошибка» имеет три различных значений, в которых люди часто путаются.
Ошибочная ситуация — непосредственно факт наличия ошибки в программе. Это может быть, например, синтаксическая ошибка (скажем, пропущенная скобка),
или же ошибка семантическая — смысловая (использование переменной, которая ранее не была определена).
Внутреннее сообщение об ошибке («внутренняя ошибка»), которую выдает PHP в
ответ на различные неверные действия программы (например, открытие несуще-
ствующего файла). Как мы знаем из гл. 23, в PHP можно устанавливать различные режимы отображения ошибок, поэтому факт наличия ошибки в программе в смысле предыдущего пункта далеко не всегда приводит к выводу сообщения
Пользовательское сообщение об ошибке («пользовательская ошибка»), к которой
причисляются все сообщения или состояния, генерируемые и обрабатываемые
