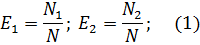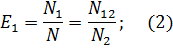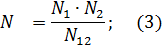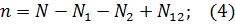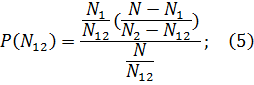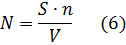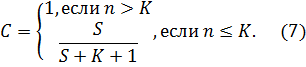Статистическая модель Миллса позволяет оценить не только количество ошибок до начала тестирования, но и степень отлаженности программ. Для применения модели до начала тестирования в программу преднамеренно вносят ошибки. Далее считают, что обнаружение преднамеренно внесенных и так называемых собственных ошибок программы равновероятно.
Для оценки количества ошибок в программе до начала тестирования используется выражение
где W ‘ — количество преднамеренно внесенных в программу ошибок до начала тестирования; V — количество обнаруженных в процессе тестирования ошибок из числа преднамеренно внесенных; S — количество «собственных» ошибок программы, обнаруженных в процессе тестирования.
Если продолжать тестирование до тех пор, пока все ошибки из числа преднамеренно внесенных не будут обнаружены, степень отлаженности программы С можно оценить с помощью выражения
где S и W = V (равенство значений W и V в данном случае имеет место, поскольку считается, что все преднамеренно внесенные ошибки обнаружены) имеют тот же смысл, что и в предыдущем выражении (2.2.1), а r означает верхний предел (максимум) предполагаемого количества «собственных» ошибок в программе.
Выражения (2.2.1) и (2.2.2) представляют собой статистическую модель Миллса. Необходимо заметить, что если тестирование будет закончено преждевременно (т. е. раньше, чем будут обнаружены все преднамеренно внесенные ошибки), то вместо выражения (2.2.2) следует использовать более сложное комбинаторное выражение (2.2.3). Если обнаружено только V ошибок из W преднамеренно внесенных, используется выражение
где в круглых скобках записаны обозначения для числа сочетаний из S элементов по V — 1 элементов в каждой комбинации и числа сочетаний из S + r + 1 элементов по r + V элементов в каждой комбинации.
Тестируя программу в течение некоторого времени и отсортировывая собственные и внесенные ошибки, можно оценить первоначальное число cобственных ошибок S в программе.
Предположим, что в программу было внесено V ошибок, после чего разрешено начать тестирование.
Пусть при тестировании обнаружено:
oS — из числа собственных ошибок программы,
oV- из числа внесенных ошибок в программу.
Тогда в среднем справедливо равенство (см. рис.)
Рис. Ошибки в программе
Следовательно, оценка для S будет такой:
Например, если в программу внесено 20 ошибок (V=20) и к некоторому моменту тестирования было обнаружено 15 собственных (oS=15) и 5 внесенных ошибок (oV=5), значение S можно оценить в 60.
Вторая часть модели связана с выдвижением и проверкой гипотез об S.
Будем утверждать, что в программе имеется не более k собсвенных ошибок. Для проверки этой гипотезы внесем в программу еще V ошибок. Протестируем программу до тех пор, пока не будут обнаружены все внесенные ошибки, причем в этот момент подсчитывается число обнаруженных собственных ошибок oS.
Уровень значимости определяется по следующей формуле:
Если число обнаруженных собственных ошибок оказалось больше числа предполагаемых то С=1, т. е. гипотеза не верна.
Если число обнаруженных собственных ошибок оказалось меньше или равно числа предполагаемых ошибок то
Чем больше число предполагаемых ошибок по сравнению с числом внесенных ошибок тем степень доверия к выдвинутой гипотезе меньше.
Например, если мы утверждаем, что в программе нет ошибок (К=0), и, внеся в программу четыре ошибки (V=4), все их обнаруживаем, не встретив ни одной собственной ошибки (oS=0), то С=0.8. Чтобы достичь уровня С=0,95, нам надо было бы внести в программу 19 ошибок.
Модель Миллса. Использование этой модели предполагает необходимость перед началом тестирования искусственно «засорять» программу
Использование этой модели предполагает необходимость перед началом тестирования искусственно «засорять» программу, т.е. вносить в нее некоторое количество известных ошибок. Ошибки вносятся случайным образом и фиксируются в проколе искусственных ошибок. Специалист, проводящий тестирование, не знает ни количества, ни характера внесенных ошибок до момента оценки показателей надежности по модели Миллса. Предполагается, что все ошибки (как естественные, так и искусственные внесены) имеют равную вероятность быть найденными в процессе тестирования.
Тестируя программу в течение некоторого времени, собирают статистику об ошибках. В момент оценки надежности по протоколу искусственных ошибок все ошибки делятся на собственные и искусственные. Соотношение, называемое формулой Миллса, дает возможность оценить первоначальное число ошибок в программе N.
Где: S – количество искусственно внесенных ошибок;
n – число найденных собственных ошибок;
V – число обнаруженных к моменту оценки искусственных ошибок.
Вторая часть модели связана с проверкой гипотезы от N. Предположим, что в программе имеется К собственных ошибок, и внесем в нее еще S ошибок. В процессе тестирования были обнаружены все S внесенных ошибок и п собственных ошибок.
Тогда по формуле Миллса мы предполагаем, что первоначально в программе было N = п ошибок. Вероятность, с которой можно высказать такое предположение, возможно рассчитать по следующему соотношению:
Таким образом, величина С является мерой доверия к модели и показывает вероятность того, насколько правильно найдено значение N.
Эти две формулы образуют полезную модель ошибок
· первая предсказывает их количество
Недостаток модели Миллса:
1. Предполагается, что собственные и внесенные ошибки обнаруживаются с одинаковой вероятностью, поэтому внесенные ошибки должны быть типичнымидля данной программы.
2. Количество внесенных ошибок должно быть в 10 раз больше, чем собственных.
3. Сложность – неизвестно, какой должна быть типичная ошибка, если тестирование проводит не тот, кто писал программу.
Поиск по сайту:
Статические модели принципиально отличаются от динамических, прежде всего тем, что в них не учитывается время появления ошибок в процессе тестирования и не используется никаких предположений о поведении функции риска
. Эти модели строятся на твердом статистическом фундаменте.
Модель Миллса. Использование этой модели предполагает необходимость перед началом тестирования искусственно вносить в программу («засорять») некоторое количество известных ошибок. Ошибки вносятся случайным образом и фиксируются в протоколе искусственных ошибок. Специалист, проводящий тестирование, не знает ни количества, ни характера внесенных ошибок до момента оценки показателей надежности по модели Миллса. Предполагается, что все ошибки (как естественные, так и искусственно внесенные) имеют равную вероятность быть найденными в процессе тестирования.
дает возможность оценить N – первоначальное число ошибок в программе. В данном соотношении, которое называется формулой Миллса, S – количество искусственно внесенных ошибок, п – число найденных собственных ошибок, V – число обнаруженных к моменту оценки искусственных ошибок.
Таким образом, величина С является мерой доверия к модели и показывает вероятность того, насколько правильно найдено значение N. Эти два связанных между собой по смыслу соотношения образуют полезную модель ошибок: первое предсказывает возможное число первоначально имевшихся в программе ошибок, а второе используется для установления доверительного уровня прогноза.
Модель Липова. Липов модифицировал модель Миллса, рассмотрев вероятность обнаружения ошибки при использовании различного числа тестов. Если сделать то же предположение, что и в модели Миллса, т.е. что собственные и искусственные ошибки имеют равную вероятность быть найденными, то вероятность обнаружения п собственных и V внесенных ошибок равна:
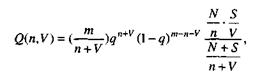
где m – количество тестов, используемых при тестировании;
q – вероятность обнаружения ошибки в каждом из m тестов, рассчитанная по формуле
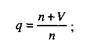
S – общее количество искусственно внесенных ошибок;
N – количество собственных ошибок, имеющихся в ПС до начала тестирования.
Для использования модели Липова должны выполняться следующие условия:
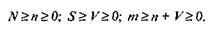
Оценки максимального правдоподобия (наиболее вероятное значение для N) задаются соотношениями
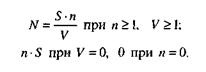
Модель Липова дополняет модель Миллса, давая возможность оценить вероятность обнаружения определенного количества ошибок к моменту оценки.
Простая интуитивная модель. Использование этой модели предполагает проведение тестирования двумя группами программистов (или двумя программистами в зависимости от величины программы) независимо друг от друга, использующими независимые тестовые наборы. В процессе тестирования каждая из групп фиксирует все найденные ею ошибки. При оценке числа оставшихся в программе ошибок результаты тестирования обеих групп собираются и сравниваются.
Получается, что первая группа обнаружила N1 ошибок, вторая – N2, a N12 – это ошибки, обнаруженные обеими группами.
Если обозначить через N неизвестное количество ошибок, присутствовавших в программе до начала тестирования, то можно эффективность тестирования каждой из групп определить как
Предполагая, что возможность обнаружения всех ошибок одинакова для обеих групп, можно допустить, что если первая группа обнаружила определенное количество всех ошибок, она могла бы определить то же количество любого случайным образом выбранного подмножества. В частности, можно допустить:
Из формулы (18) N2 = E2N, подставив в (19), получим:
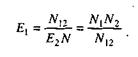
Модель Коркорэна. Модель Коркорэна относится к статическим моделям надежности ПС, так как в ней не используются параметры времени тестирования и учитывается только результат N испытаний, в которых выявлено Ni ошибок i–го типа. Модель использует изменяющиеся вероятности отказов для различных типов ошибок.
В отличие от двух рассмотренных выше статических моделей, по модели Коркорэна оценивается вероятность безотказного выполнения программы на момент оценки:
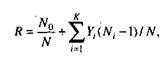
где N0 – число безотказных выполнений программы; N – общее число прогонов; К – априори известное число типов.
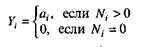
аi – вероятность выявления при тестировании ошибки i–го типа.
В этой модели вероятность аi должна оцениваться на основе априорной информации или данных предшествующего периода функционирования однотипных программных средств.
Модель Нельсона. Данная модель при расчете надежности ПС учитывает вероятность выбора определенного тестового набора для очередного выполнения программы.
На практике вероятность выбора очередного набора данных для прогона (Pi) определяется путем разбиения всего множества значений входных данных на подмножества и нахождения вероятностей того, что выбранный для очередного прогона набор данных будет принадлежать конкретному подмножеству. Определение этих вероятностей основано на эмпирической оценке вероятности появления тех или иных входов в реальных условиях функционирования.
Показатели ремонтопригодности
- Вероятность безотказной работы — вероятность того, что в пределах заданной наработки отказ системы не возникнет.
- Вероятность отказа — обратная величина, вероятность того, что в пределах заданной наработки отказ системы возникнет.
- Средняя наработка до отказа — математическое ожидание наработки системы до первого отказа (существенно для невосстанавливаемых систем).
- Средняя наработка на отказ (То, MTBF — Main Time Between Failures) — отношение наработки восстанавливаемой системы к математическому ожиданию числа ее отказов в пределах этой наработки (имеет смысл только для восстанавливаемых систем).
- Интенсивность отказов — условная плотность вероятности возникновения отказа невосстанавливаемой системы, определяемая для рассматриваемого момента времени при условии, что до этого момента отказ не возник.
- Параметр потока отказов (X(t)) — отношение среднего числа отказов для восстанавливаемой системы за произвольно малую ее наработку к значению этой наработки.
- Средний ресурс — математическое ожидание наработки системы от начала ее эксплуатации или ее возобновления после ремонта до перехода в предельное состояние.
- Срок службы (Tcc) — календарная продолжительность от начала эксплуатации системы или ее возобновления после ремонта до перехода в предельное состояние.
- Комплексные показатели надежности.
- Вероятность восстановления работоспособного состояния — вероятность того, что время восстановления работоспособного состояния не превысит заданного.
- Среднее время восстановления работоспособного состояния (Tв) — математическое ожидание времени восстановления работоспособного состояния системы.
В стандарте ISO 9126 надежность определяется как, способность программного обеспечения выполнять свои функции в заданных условиях. При этом это свойство составляется такими элементами:
- Зрелость (величина, обратная частоте критических отказов, вызванных ошибками в ПО).
- Устойчивость к отказам (способность поддерживать заданный уровень работоспособности при внутренних и внешних отказах).
- Способность к восстановлению (способность восстанавливать определенный уровень работоспособности и целостность данных после отказа).
- Соответствие стандартам надежности.
Проблема надежности имеет две стороны: оценка и обеспечение. Рассмотрим первую. Она решается применением моделей. Их можно классифицировать, прежде всего, на две группы: аналитические и эмпирические. Первые в свою очередь делятся на две группы: статические и динамические. Первые из них (статические) рассчитывая соответствующие метрики непосредственно, а вот вторые (динамические) — используют прогнозные модели. И первой, и во второй группе можно привести 6 конкретных моделей.
Исходные данные для динамических моделей дискретного времени, собираются в процессе тестирования ПС в течение фиксированных или случайных временных интервалов. Каждый интервал – это стадия, на которой выполняется последовательность тестов и фиксируется некоторое число ошибок.
Динамическая модель непрерывного времени означает, что в процессе тестирования фиксируется время выполнения программы (тестового прогона) до очередного отказа. Но считается, что не всякая ошибка ПС может вызвать отказ, поэтому допускается обнаружение более одной ошибки при выполнении программы до возникновения очередного отказа.
Несмотря на очевидную актуальность, вопрос оценки надежности программного обеспечения не привлекает должного внимания. Вместе с тем, даже поверхностный анализ проблемы с теоретико-вероятностной точки зрения позволяет выявить некоторые закономерности.
Модель Шумана. Исходные данные для модели Шумана, которая относится к динамическим моделям дискретного времени, собираются в процессе тестирования ПС в течение фиксированных или случайных временных интервалов. Каждый интервал – это стадия, на которой выполняется последовательность тестов и фиксируется некоторое число ошибок.
Модель Шумана может быть использована при определенным образом организованной процедуре тестирования. Использование модели Шумана предполагает, что тестирование проводится в несколько этапов. Каждый этап представляет собой выполнение программы на полном комплексе разработанных тестовых данных. Выявленные ошибки регистрируются (собирается статистика об ошибках), но не исправляются. По завершении этапа на основе собранных данных о поведении ПС на очередном этапе тестирования может быть использована модель Шумана для расчета количественных показателей надежности. После этого исправляются ошибки, обнаруженные на предыдущем этапе, при необходимости корректируются тестовые наборы и проводится новый этап тестирования. При использовании модели Шумана предполагается, что исходное количество ошибок в программе постоянно и в процессе тестирования может уменьшаться по мере того, как ошибки выявляются и исправляются. Новые ошибки при корректировке не вносятся. Скорость обнаружения ошибок пропорциональна числу оставшихся ошибок. Общее число машинных инструкций в рамках одного этапа тестирования постоянно.
Предполагается, что до начала тестирования в ПС имеется Ет ошибок. В течение времени тестирования
Таким образом, удельное число ошибок на одну машинную команду, оставшихся в системе после времени тестирования
где IТ – общее число машинных команд, которое предполагается постоянным в рамках этапа тестирования.
Автор предполагает, что значение функции частоты отказов Z(t) пропорционально числу ошибок, оставшихся в ПС после израсходованного на тестирование времени
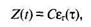
где С – некоторая константа; t – время работы ПС без отказа.
Тогда, если время работы ПС без отказа t отсчитывается от точки t = 0, а
Из величин, входящих в формулы (2) и (3), не известны начальное значение ошибок в ПС (Ет) и коэффициент пропорциональности С. Для их определения прибегают к следующим рассуждениям. В процессе тестирования собирается информация о времени и количестве ошибок на каждом прогоне, т.е. общее время тестирования
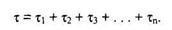
Предполагая, что интенсивность появления ошибок постоянна и равна l, можно вычислить ее как число ошибок в единицу времени:
где Аi – количество ошибок на i–м прогоне;
Имея данные для двух различных моментов тестирования
, которые выбираются произвольно с учетом требования, чтобы
, можно сопоставить уравнения (3) и (5) при
Вычисляя отношения (6) и (7), получим:
Подставив полученную оценку параметров EТ в выражение (6), получим оценку для второго неизвестного параметра:
Получив неизвестные EТ и С, можно рассчитать надежность программы по формуле (2).
Модель La Padula. По этой модели выполнение последовательности тестов производится в m этапов. Каждый этап заканчивается внесением изменений (исправлений) в ПС. Возрастающая функция надежности базируется на числе ошибок, обнаруженных в ходе каждого тестового прогона.
Надежность ПС в течение i –го этапа:
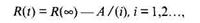
где А – параметр роста;
Эти неизвестные величины автор предлагает вычислить, решив следующие уравнения:
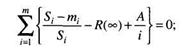
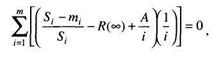
где Si – число тестов;
m – число этапов;.
Преимущество модели заключается в том, что она является прогнозной и, основываясь на данных, полученных в ходе тестирования, дает возможность предсказать вероятность безотказной работы программы на последующих этапах ее выполнения.
Модель Джелинского – Моранды. Модель Джелинского – Моранды относится к динамическим моделям непрерывного времени. Исходные данные для использования этой модели собираются в процессе тестирования ПС. При этом фиксируется время до очередного отказа. Основное положение, на котором базируется модель, заключается в том, что значение интервалов времени тестирования между обнаружением двух ошибок имеет экспоненциальное распределение с частотой ошибок (или интенсивностью отказов), пропорциональной числу еще не выявленных ошибок. Каждая обнаруженная ошибка устраняется, число оставшихся ошибок уменьшается на единицу.
Функция плотности распределения времени обнаружения i –й ошибки, отсчитываемого от момента выявления (i–1)–й ошибки, имеет вид:
– частота отказов (интенсивность отказов), которая пропорциональна числу еще не выявленных ошибок в программе.
где N – число ошибок, первоначально присутствующих в программе;
С – коэффициент пропорциональности.
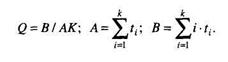
Поскольку полученные значения
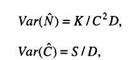
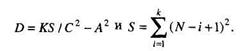
Чтобы получить числовые значения
, нужно подставить вместо N и С их возможные значения
Модель Шика – Волвертона. Модификация модели Джелинского – Моранды для случая возникновения на рассматриваемом интервале более одной ошибки предложена Волвертоном и Шиком. При этом считается, что исправление ошибок производится лишь после истечения интервала времени, на котором они возникли. В основе модели Шика – Волвертона лежит предположение, согласно которому частота ошибок пропорциональна не только количеству ошибок в программах, но и времени тестирования, т.е. вероятность обнаружения ошибок с течением времени возрастает. Частота ошибок (интенсивность обнаружения ошибок)
, предполагается постоянной в течение интервала времени ti и пропорциональна числу ошибок, оставшихся в программе по истечении (i–1)–го интервала; но она пропорциональна также и суммарному времени, уже затраченному на тестирование (включая среднее время выполнения программы в текущем интервале):
В данной модели наблюдаемым событием является число ошибок, обнаруживаемых в заданном временном интервале, а не время ожидания каждой ошибки, как это было для модели Джелинского – Моранды. В связи с этим модель относят к группе дискретных динамических моделей.
Модель Муса. Модель Муса относят к динамическим моделям непрерывного времени. Это значит, что в процессе тестирования фиксируется время выполнения программы (тестового прогона) до очередного отказа. Но считается, что не всякая ошибка ПС может вызвать отказ, поэтому допускается обнаружение более одной ошибки при выполнении программы до возникновения очередного отказа.
Считается, что на протяжении всего жизненного цикла ПС может произойти M0 отказов и при этом будут выявлены все N0 ошибки, которые присутствовали в ПС до начала тестирования.
Общее число отказов M0 связано с первоначальным числом ошибок N0 соотношением
где В – коэффициент уменьшения числа ошибок.
В момент, когда проводится оценка надежности, после тестирования, на которое потрачено определенное время t, зафиксировано m отказов и выявлено п ошибок.
Тогда из соотношения
можно определить коэффициент уменьшения числа ошибок В как число, характеризующее количество устраненных ошибок, приходящихся на один отказ.
В модели Муса различают два вида времени:
1) суммарное время функционирования
, которое учитывает чистое время тестирования до контрольного момента, когда проводится оценка надежности;
2) оперативное время t – время выполнения программы, планируемое от контрольного момента и далее при условии, что дальнейшего устранения ошибок не будет (время безотказной работы в процессе эксплуатации).
Для суммарного времени функционирования
– интенсивность отказов пропорциональна числу неустраненных ошибок;
– скорость изменения числа устраненных ошибок, измеряемая относительно суммарного времени функционирования, пропорциональна интенсивности отказов.
Один из основных показателей надежности, который рассчитывается по модели Муса, – средняя наработка на отказ. Этот показатель определяется как математическое ожидание временного интервала между последовательными отказами и связан с надежностью:
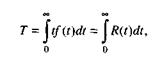
где t – время работы до отказа.
Если интенсивность отказов постоянна (т.е. когда длительность интервалов между последовательными отказами имеет экспоненциальное распределение), то средняя наработка на отказ обратно пропорциональна интенсивности отказов.
Модель переходных вероятностей. Эта модель основана на марковском процессе, протекающем в дискретной системе с непрерывным временем.
Процесс, протекающий в системе, называется марковским (или процессом без последствий), если для каждого момента времени вероятность любого состояния системы в будущем зависит только от состояния системы в настоящее время (to) и не зависит от того, каким образом система пришла в это состояние. Процесс тестирования ПС рассматривается как марковский процесс.
В начальный момент тестирования (t = 0) в ПС было n ошибок. Предполагается, что в процессе тестирования выявляется по одной ошибке. Тогда последовательность состояний системы (n, n–1, n–2, n–3) и т.д. соответствует периодам времени, когда предыдущая ошибка уже исправлена, а новая еще не обнаружена. Например, в состоянии n–5 пятая ошибка уже исправлена, а шестая еще не обнаружена.
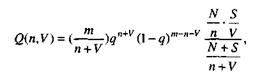

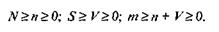
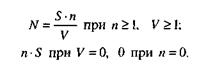
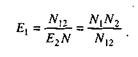
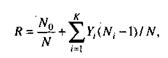
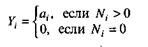
уточнения плановых сроков завершения проекта и т.д.
Под программным модулем в данном случае следует понимать программную единицу, выполняющую определенную функцию (ввод, вывод, вычисление и т.д.) и взаимосвязанную с другими модулями ПС. Сложность модуля ПС может быть описана, если рассматривать структуру программы.
В качестве структурных характеристик модуля ПС используются:
1 отношение действительного числа дуг к максимально возможному числу дуг, получаемому искусственным соединением каждого узла с любым другим узлом дугой;
2 отношение числа узлов к числу дуг;
3 отношение числа петель к общему числу дуг.
Для сложных модулей и для больших многомодульных программ составляется имитационная модель, программа которой «засоряется» ошибками и тестируется по случайным входам. Оценка надежности осуществляется по модели Миллса.
При проведении тестирования известна структура программы, имитирующей действия основной, но не известен конкретный путь, который будет выполняться при вводе определенного тестового входа. Кроме того, выбор очередного тестового набора из множества тест–входов случаен, т.е. в процессе тестирования не обосновывается выбор очередного тестового входа. Эти условия вполне соответствуют реальным условиям тестирования больших программ.
Полученные данные анализируются, проводится расчет показателей надежности по модели Миллса (или любой другой из описанных выше), и считается, что реальное ПС, выполняющее аналогичные функции, с подобными характеристиками и в реальных условиях должно вести себя аналогичным или похожим образом.
Преимущества оценки показателей надежности по имитационной модели, создаваемой на основе анализа структуры будущего реального ПС, заключаются в следующем:
– модель позволяет на этапе проектирования ПС принимать оптимальные проектные решения, опираясь на характеристики ошибок, оцениваемые с помощью имитационной модели;
— модель позволяет прогнозировать требуемые ресурсы тестирования;
– модель дает возможность определить меру сложности программ и предсказать возможное число ошибок и т.д.
К недостаткам можно отнести высокую стоимость метода, так как он требует дополнительных затрат на составление имитационной модели, и приблизительный характер получаемых показателей.
Модель, определяющая время доводки программ. Эта модель используется для ПС, которые имеют иерархическую структуру, т.е. ПС как система может содержать подсистемы, которые состоят из компонентов, а те, в свою очередь, состоят из W модулей. Таким образом, ПС может иметь W различных уровней композиции. На любом уровне иерархии возможна взаимная зависимость между любыми парами объектов системы. Все взаимозависимости рассматриваются в терминах зависимости между парами модулей.
Анализ модульных связей строится на том, что каждая пара модулей имеет конечную (возможно, нулевую) вероятность, изменения в одном модуле вызовут изменения в другом модуле.
Данная модель позволяет на этапе тестирования, а точнее при тестовой сборке системы, определять возможное число необходимых исправлений и время, необходимое для доведения ПС до рабочего состояния.
Основываясь на описанной процедуре оценки общего числа изменений, требуемых для доводки ПС, можно построить две различные стратегии корректировки ошибок:
– фиксировать все ошибки в одном выбранном модуле и устранить все побочные эффекты, вызванные изменениями этого модуля, отрабатывая таким образом последовательно все модули;
– фиксировать все ошибки нулевого порядка в каждом модуле, затем фиксировать все ошибки первого порядка и т.д.
Исследование этих стратегий доказывает, что время корректировки ошибок на каждом шаге тестирования определяется максимальным числом изменений, вносимых в ПС на этом шаге, а общее время – суммой максимальных времен на каждом шаге. Это подтверждает известный факт, что тестирование обычно является последовательным процессом и обладает значительными возможностями для параллельного исправления ошибок, что часто приводит к превышению затрачиваемых на него ресурсов над запланированными.
Задачи по применению модели Миллса
В программу преднамеренно внесли (посеяли) 10 ошибок. В результате тестирования обнаружено 12 ошибок, из которых 10 ошибок были внесены преднамеренно. Все обнаруженные ошибки исправлены. До начала тестирования предполагалось, что программа содержит не более 4 ошибок. Требуется оценить количество ошибок до начала тестирования и степень отлаженности программы.
Для оценки количества ошибок до начала тестирования используем формулу (1). Нам известно:
· количество «собственных» ошибок в программе n = 12 — 10 = 2.
Подставив указанные значения в формулу, получим оценку количества ошибок:
Таким образом, из результатов тестирования следует, что до начала тестирования в программе имелось 2 ошибки.
Для оценки отлаженности программы используем уравнение (2). Нам известно:
Очевидно, что обнаружено меньшее число «собственных» ошибок, чем количество предполагаемых ошибок в программе (n С = S /(S+K + 1) = 10/(10 + 4+ 1) = 0,67 Степень отлаженности программы равна 0,67, что составляет 67%. В программу было преднамеренно внесено (посеяно) 7 ошибок. В результате тестирования обнаружено 11 ошибок, из которых 7 ошибок были внесены преднамеренно. Все обнаруженные ошибки исправлены. До начала тестирования предполагалось, что программа содержит не более 5 ошибок. Требуется оценить количество ошибок до начала тестирования и степень отлаженности программы. Подставив указанные значения в формулу, получим оценку: Таким образом, из результатов тестирования следует, что до начала тестирования в программе имелось 4 ошибки. Очевидно, что обнаружено меньшее число «собственных» ошибок, чем количество предполагаемых ошибок в программе (n < K). Для оценки отлаженности программы используем уравнение С= S/(S+K + 1) = 7/(7 + 5 + 1) = 0,54 Степень отлаженности программы равна 0,54, что составляет 54%. В программу было преднамеренно внесено (посеяно) 14 ошибок. Предположим, что в программе перед началом тестирования было 14 ошибок. В процессе четырех тестовых прогонов было выявлено следующее количество ошибок. Необходимо оценить количество ошибок перед каждым тестовым прогоном. Оценить степень отлаженности программы после последнего прогона. Построить диаграмму зависимости возможного числа ошибок в данной программе от номера тестового прогона. Количество ошибок перед каждым прогоном будем оценивать в соответствии с выражением (1). Перед каждой последующей оценкой количества ошибок и степени отлаженности программы необходимо корректировать значения внесенных S и предполагаемых K ошибок с учетом выявленных и устраненных после каждого прогона тестов. Степень отлаженности программы на всех прогонах, кроме последнего, рассчитывается по комбинаторной формуле. Определяя показатели программы по результатам первого прогона, необходимо учитывать, что S 1 = 14; n 1 = 4; V 1 = 6, тогда N1 = (S1*n1)/ V1= (14 * 4) / 6 = 9 По результатам второго прогона корректируем исходные данные для оценки параметров: K2 = 14 — 4 = 10; S 2 = 14 — 6 = 8; n 2 = 2; V2 = 4, следовательно, N2 = (S2*n2)/V2 = (8*2)/4 = 4. Корректировка исходных данных после третьего прогона дает следующие данные: K 3 = 10 — 2 = 8, S 3 = 8 — 4 = 4; n 3= 1; V 3 = 2, откуда количество ошибок определится следующим образом: N3 = (S3*n3)/V3 = (4*1)/2 = 2. После четвертого прогона программы получим следующие исходные данные: K4 = 8 — 1 = 7, S4 = 4 — 2 = 2; n4 = 1; V4 = 2, тогда N4 = (S4 *n 4) / V4 = (2 * 1) / 2 = 1. Поскольку после четвертого прогона все «посеянные» ошибки выявлены и устранены, то для оценки отлаженности программы можно воспользоваться упрощенной формулой C=S/(S+K + 1) = 2/(2 + 7+ 1) = 0,2. Таким образом, в предположении, что до начала четвертого прогона в программе оставалось 7 ошибок, степень отлаженности программы составляет 20%. Результат по количеству ошибок в программе до начала каждого прогона приведен ниже. На приведенном графике дополнительно отображена линия тренда, характеризующая тенденцию снижения количества ошибок в программе по результатам тестовых прогонов. Рисунок 2. Динамика количества ошибок при тестировании программы В программу было преднамеренно внесено (посеяно) 14 ошибок. В результате тестирования обнаружено 9 ошибок, из которых 6 ошибок были внесены преднамеренно. Все обнаруженные ошибки исправлены. До начала тестирования предполагалось, что программа содержит не более 4 ошибок. Требуется оценить степень отлаженности программы на момент завершения тестирования. Если тестирование закончено раньше, чем обнаружены все преднамеренно внесенные ошибки, то следует применять более сложное комбинаторное выражение (6). Из условия задачи нам известно: · количество внесенных в программу ошибок S =14; Подставив значения в формулу, получим оценку количества ошибок: Таким образом, из результатов тестирования следует, что до начала тестирования в программе имелось 7 ошибок. Для оценки отлаженности программы используем уравнение (7). Нам известно: · количество преднамеренно внесенных и обнаруженных ошибок S = 14. С = S /(S+K + 1) = 14/(14 + 4+ 1) = 0,74 Степень отлаженности программы равна 0,74, что составляет 74%. В проделанной нами работе была достигнута первоначально поставленная цель. Мы изучили статические модели и метрики для определения качества ПО. Для достижения данной цели мы ознакомились с показателями качества программного обеспечения по стандарту ГОСТ Р 9126-93. Изучили статические модели и метрики. Для лучшего представления и анализа рассмотрели модели Миллса и простую интуитивную модель на конкретных примерах. Следует признать, что абсолютно надежных программ не существует, так как абсолютная степень надежности не может быть теоретически доказана и, следовательно недостижима. Однако важно знать, насколько надежно конкретное ПО. Описанные модели представляют теоретический подход и, как правило, имеют ограниченное применение. До сих пор не предложено ни одного надежного количественного метода оценки надежности ПО, не содержащего чрезмерного количества ограничений. Практика разработки ПО предполагает приоритет задачи обеспечения надежности над задачей её оценки. Ситуации выглядит парадоксально: совершенно очевидно, что прежде чем обеспечивать надежность, следует научиться её измерять. Но для этого нужно иметь практически приемлемую единицу измерения надежности ПО и модели её расчета. Пусть в процессе тестирования обнаружено n исходных ошибок и v из S рассеянных ошибок. Тогда оценка N — первоначальное число ошибок в программе — составит Вторая часть модели связана с проверкой гипотезы выражения и тестирования N. Рассмотрим случай, когда программа содержит К собственных ошибок и S рассеянных ошибок. Будем тестировать программу до тех пор, пока не обнаружим все рассеянные ошибки. В то же время количество обнаруженных исходных ошибок накапливается и запоминается. Далее вычисляется оценка надежности модели: как вероятность того, что в программе содержится K ошибок. Формула для расчета С в случае, когда обнаружены не все искусственно рассеянные ошибки, модифицирована таким образом, что оценка может быть выполнена после обнаружения v (v£S) рассеянных ошибок: где числитель и знаменатель формулы при n £ К являются биноминальными коэффициентами. Предположим, что в программе имеется 3 собственных ошибки. Внесём ещё 6 ошибок случайным образом. В процессе тестирования было найдено: 1) 6 ошибок из рассеянных и 2 собственных; 2) 5 ошибок из рассеянных и 2 собственных; 3) 5 ошибок из рассеянных и 4 собственных. Найти надёжность по модели Миллса — С. 1) n=2, v=6, C=(6!/(6-1)!)/((6+3+1)!/(3+6)!)=0,6. 2) n=2, v=5, C=(6!/(5-1)!)/((6+3+1)!/(3+5)!)=0,333333, 2!=2, 4!=24, 6!=720, 8!=40320, 10!=3628800. 3) n=4, v=5, C=1 (по формуле (18)). mydocx.ru — 2015-2023 year. (0.006 sec.) Где N – неизвестное количество ошибок, присутствовавших в программе до начала тестирования; N1 – количество ошибок найденных первой группой тестеров; N2 – количество ошибок найденных второй группой тестеров; N12 – ошибки обнаруженные дважды (обеими группами); Е – эффективность тестирования; Эффективность тестирования каждой из групп можно определить как Предполагая, что возможность обнаружения всех ошибок одинакова для обеих групп можно допустить, что если первая группа обнаружила определенно количество всех ошибок, она могла бы определить то ж0е количество любого случайным образом выбранного подмножества. В частности, можно допустить из формулы (2) получим Число оставшихся ошибок можно найти как Вероятность обнаружения общих ошибок: Примеры решения задачПростая интуитивная модель